By Steven M. Smith

"The beautiful is a manifestation of the secret laws of nature... When nature begins to reveal her open secret to a person, he feels an irresistible longing for her most worthy interpreter, art."

- Johann Wolfgang von Goethe- early color theorist

Introduction

Numbers are the basis of mathematics and counting. They are universal, being used by humans in their daily lives. By visualizing number systems, I turn the abstract idea of counting into an image of patterning. I materialize a pre-defined arrangement. The grids and patterns in Color by Numbers systemic structures are innate to math and geometry and both have fractal principles.

I have realized that counting itself is a fractal principal. It has repetition, self-similarity, iteration, and infinity. Counting may be the earliest fractal man ever invented. It has been latent in the face of mathematicians and scientists for ages. I feel it is time to explore counting’s multi-dimensional ramifications. I am not particularly interested in numerology, but that could also be used to create number patterns using these systemic approaches.

Counting can be expressed through color (and other variables as well). Simply assign a variable to a number and count to get periodic, infinitely variable arrays, with a certain amount of control. When imposed on grid surfaces, these structures can be expressed as static visuals. By assigning color to number, I have been exploring and searching for new dimensions of patterning. I am also pursuing the beauty, synchronicity and coherence of number systems in these structures.

Color by Numbers (CBN)

CBN mixes fundamental mathematics with fundamental geometry as it creates color fractals. CBN is a methodology for patterning regular geometric structures with counting patterns using colors. Colors are mapped to numbers which array linear pattern sequences on grids.

We can program computers to graph the resulting patterns. We can also do this directly with physical media, turning a canvas (or other media) into a sort of handmade computer for patterns. The results are predetermined after the initial choice of colors and arrangement. There is an broad freedom in choosing the colors, the number base (which is the number of colors), the way they are arranged and on what surface structure they are arranged, and the media used to express this patterning. The resulting pattern spreads magically to the surface and inundates it with a visual result.

CBN Painting Base 8 Octagon, 1 to 1000, Blended, 2011

Number Bases:

You can count (colorize) in various number bases depending on how many various elements you would like to work with. Base 10 uses 10 colors, Base 2 uses 2 colors, etc. Below is an example of a base 2 array of counting presented as if reading a book (left to right, jumping to the next line down vertically).

Early Pen Plot Base 2 sequential digits, 1979.

Note that counting thresholds (ie. Hitting 1,000) are abrupt and can form into columns depending on the width of the structure and the number of digits involved in displaying each numeral. Number bases can be utilized to limit the seeding of the pattern with a palette of colors equal to the number base. This increases the creative possibilities greatly. Grid elements can easily include other structures than just color.

For example, I have created patterns from counting with letters in base 26 (the alphabet) that include all possible words (as well as all unused letter combinations) from that alphabet. This creates a word database that is comprehensive, organized and searchable for mild deviations.

For clarity, I am talking about counting in other number bases than our familiar base 10. Binary - base 2 is an obvious example, but for all readers whose math is fuzzy in this esoteric area, it goes something like this: Counting in base 4 would have us think of 3 as we would 9, only 3 would trigger the next threshold of counting. 9 is the end of a sequence of 10 – don’t forget about zero as a digit – the most improbable of numbers. Base 4 has 4 colors (elements) representing the digits 0, 1, 2, 3.

Let’s look at this as a sequential array of digits:

1 2 3 1 0 1 1 1 2 1 3 2 0 2 1 2 2 2 3 3 0 3 1 3 2 3 3 3 1 0 0 1 0 1 …

And now as a sequence of numbers:

1 2 3 10 11 12 13 20 21 22 23 30 31 32 33 100 101 …

These create 2 linear possibilities of counting with colors –

Sequential digits (now in Base 10):

If red represents 1 and orange represents 1, 12 could be represented by red followed by orange

Blended colors from the mix of the digits of the numeral.

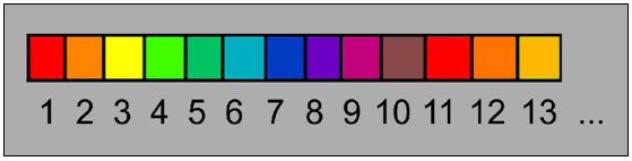
Current counted numeral is represented by blended digits – Color 13 equals even quantities of 1 and 3 on one color chip (grid element). This generates mostly new colors as we count. Some remain the same – 123, 231, and 321 are the same blended color.

My first explorations with Coloring by Numbers quickly led to a partnership with Jeff Yetter from Hewlett Packard who assisted me in programming early HP machines to create counting patterns in 1979. I had created numerous hand drawings and had been using a limited number of colors in a certain number base. We used sequential counting in these explorations partially because we had a limited amount of colors. This was an excellent match for a pen plotter; which was the only available high resolution output at the time, considering raster graphics was at its infancy (mostly black and white).

Example of Early Pen Plot – Arrangement reads like a book, 1980.

Example of blended colors, Acrylic on Canvas, 2011.

Grid structures and arrangement on grid surface:

I am launched into an exploration of grids by necessity when creating a static image representation of counting patterns. Temporal exploration without grids is, of course, another possibility. I am sure there are formats to explore that involve no grids.

My visual representations have been created within the physical limits of a grid at a certain size and detail. Therefore grids can give birth to larger, conceptual grids as they imply an expansion towards infinity past their container. We can explore pre-defined counting patterns by birthing our own arrangements and color choices on grids. Linear number sequences could read like a book, wrap around themselves in spirals, read left-right/right-left, array in plaid form or move through 3D space (or whatever we decide).

Square Grids:

Square grids are the most common grids. They are implicit in 2 dimensional coordinate systems. They were the first I explored. I quickly decide to spiral from the center as it easily implied the continuity on the grid towards infinity.

Acrylic Painting on Canvas, Blended colors, 1990

The first 1 million numbers of base 10, blended and arrayed like a book. 2013 from CBN blaster code.

Pattern by Numbers:

Rather than just a color, a pattern and a color can be applied to the grid. There are infinite possibilities here as well.

Pen plot – Pattern by Numbers Series, 1980

Lines and Plaids:

Sequences of lines can be used in counting. This has worked well for weaving and simple drawings. There are infinite variations on this theme alone, considering the variables of color choice, number bases, and range of counting activity (what number you start and end with).

5 Drawings – Pen on Paper, 1988.

Another logical use of square grids with a linear sequence is to create plaids by repeating the sequence as horizontal and vertical line sequences combined.

Pen plot – Plaid Waves Series, 1980

Polygonal Grids:

Watercolor series for Master’s Thesis - Base 3 triangle, base 4 square, base 5 pentagon, base 6 hexagon,….., 1982

Polygonal grids were inspired by tessellation geometry and optical illusions. Continuing the patterns beyond the viewing surface, the viewer can mentally continue the pattern (with some effort). This implied continuation infers and compels the infinite expansion that is possible. Polygonal grids can subdivide most any polygon and that is another realm to explore. These grids are fractals themselves.

Most of my explorations of CBN involve grids wherein I begin from the center and spiral outward, usually clockwise. CBN spirals usually represent the inception of an infinite field of patterned colors (radiating outward) - limited by the edge and size of the grid.

Color and Pattern by Numbers Pen plot – Folded Poly Series, 1980

Tessellating CBN pen plot with colored pencil – Plaid Waves Series, 1980

Choice of media:

Media choice adds another arena of variables for CBN. Colors, patterns, images, audio or video bits can represent the digits of the numbers or can be mixed to represent complete integers. Click on this link for an example of audio I edited using CBN. My apologies to Julie Andrews and the Sound of Music.

download do me me re so so.mp3

Though using a computer is more accurate, pleasing patterns can be created with colored pencils on graph paper or with grid-based media such as mosaic tile, weaving, hook rugs, and needlepoint. Many modular systems and tessellations are ripe for this kind of patterning.

Glass Mosaic Color by Numbers Pyramid , 2011.

Color and Pattern by Numbers Needlepoint, Base 10, 1985.

Color by Numbers Hook Rug - Base 10, 2011.

Computer Graphics:

One of the major media I have used to explore CBN is Computer Graphics.

“To assert that computer assisted art is not art is as absurd as saying that computer assisted music is not music.” - Steve Smith, 1982

Color by Numbers Screen Photograph – Early Raster Graphics, 1982.

Utilizing simple mathematics, I can program a pattern into traditional media. The color choices act as a seed to the overall design and, pre-ordained, dictate the final outcome. These ideas can add meaning to abstract art. Natural counting structures can be analyzed and appreciated.

Objectifying art into systems (systemic art) can minimize spontaneity and expression. A certain diligence is required to execute drawings of systemic structures. One factor for me is keeping count. These factors open the door for the use of a computer to execute the final drawing. Computers are precise, consistent, versatile, accurate and tireless. They cannot be ignored as valid tools for visual artists. With their use comes a certain loss of individuality and a denial of handcraftsmanship, but computer graphics has the potential to map realities that go beyond human capability (by hand). The drawing below is a good example of the accuracy that would be impossible manually.

Color by Numbers Pen Plot – Plaid Waves Series, 1980.

This work with pen plotters using 3D grids in perspective is an illustration of an impossible task for the human hand to execute. Even the best draftsman could not execute these drawings. The computer can output this work with a speed and perfection which is alarming.

Perfection becomes the norm. Human skill is evident, not in execution or expression, but in the structure, concept and color choices. One program can be used to create endless variations on one idea or arrangement, with minimal time and effort.

Just seed the chart and let it go (see the supplied executable for an example of many drawn versions).

Download CBN Blaster.wmv

3D graphics and animation are areas I have dedicated a lot of time to explore.

Still from “Shapecube” 3D Animation – Cube Plaid Series, 2012.

Click here to download - Shapecube.avi - animation

CBN for Science:

CBN is a regulated, apparent random, way of mixing colors. This can be used to chart subtle variations in color mixing, including all (actually this is infinite) possible mixing of any set of colors. Out to infinity, any subtle layer can be analyzed by zooming in on that numeric section of the counting pattern. An application for color matching and paint mixing is one area of possibilities. Existing colors can be matched with only a certain, limited number of source colors. An example would be a paint store that is out of a certain base pigment. Perhaps there is an available substitute – the exact proportions of the existing pigments just need to be determined.

CBN simulates randomness with user controls available at many levels. Numbers can be charted and displayed with a seeming randomness. This could have many scientific and other useful ramifications. It could augment or replace a scientific dependence on random number generation and add a stable, chartable substructure. This could track a set number of variables (or constants) in a database that charts all possible combinations of those variables (or constants).

QR (Quick Response) Codes are a new phenomenon. Perhaps CBN could yield color variations with multiple levels of information concurrently. This idea was aroused by the fact that QR codes remind me of my early CBN explorations.

Left: QR code for ArtToyz.com, 2011; Right: CBN base 2 from Visual basic program, 1999

There are perhaps unrealized applications to science and other fields. I invite readers to pursue any ideas along these lines and I would be glad to assist in such undertakings.

Artistic Influences:

CBN influences include a mixture of science, art and religion. One of my artistic influences for CBN includes elements of Tibetan Art – Yantra and Mandala. M.C. Escher’s grid studies from the Alhambra were a major influence on my conception of periodic, triangular grid structures. The 60’s spawned many ideas: Conceptual Art (Sol LeWitt), Op Art (Victor Vasarely) and Blacklight (Dayglo) Art. Note that most of the paintings I have done in the last few years mix blacklight pigment with regular pigments to create gradations of blacklight effects. This expands beyond the traditional colors that can be reproduced through printing, computer graphics or photography as they are outside the gamut of RGB or CMYK. It also means the paintings look completely different in a blacklight.

Sri Yantra, from Wikipedia

– Note the vibrations and eye-wandering in the center triangles.

Sol LeWitt, All Single, Double, Triple, and Quadruple Combinations of Lines in Four Directions One-, Two-, Three- and Four-Part Combinations (for Center Spread/Art and Project), 1969

Victor Vasarely, Circa 1970, from Google image search

I am currently exploring octaves and harmonic structures. I have started using rainbows of colors. Vibrational relationships and scales of colors are being explored with subtle filtration and mixture. My goal is to seek coherence in the patterning.

Obviously the artistic possibilities are endless. CBN is multi-dimensional. Colors’ individual properties fit together with natural weighting toward coherence. Perhaps we can materialize harmonic structures and scales – such as music utilizes. Color vibration is just like scales in music – but faster.

These numeric sequences could also be presented in temporal arrangements to create audio and video. We can make our own rules and use numbers however we want. Maybe the Fibonacci

sequence, maybe primes, primes backward, ... Note: there is no requirement to count forwards (or to start with 1).

Please help me explore these new realms of pattern structures. The images and software on this website are free of charge AND copyright restrictions. Collaboration and creative use of CBN are welcomed.

“The universality of Number can be seen in another, more physical context. We learn from modern physics that from gravity to electromagnetism, light, heat, and even in what we think of as solid matter itself, the entire perceptible universe is composed of vibrations, perceived by us as wave phenomena. Waves are pure temporal patterns, that is dynamic configurations composed of amplitude, interval and frequency, and they can be defined and understood by us only through Number. Thus our whole universe is reducible to Number.

- Robert Lawlor, Philosophy and Practice Sacred Geometry

Steve Smith 1/2013

Links:

http://www.ArtToyz.com

http://www.sacred-geometry.com/index.html

http://www.halexandria.org/dward095.htm